A Bayesian Framework for Causal Analysis of Recurrent Events with Timing Misalignment
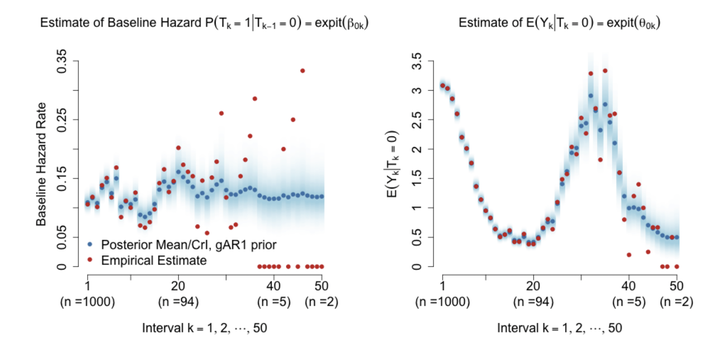 Bayesian semiparametric baseline hazard (left) and event rate (right) under gAR1 smoothing priors.
Bayesian semiparametric baseline hazard (left) and event rate (right) under gAR1 smoothing priors.
Abstract
Observational studies of recurrent event rates are common in biomedical statistics. Broadly, the goal is to estimate differences in event rates under two treatments within a defined target population over a specified followup window. Estimation with observational data is challenging because, while membership in the target population is defined in terms of eligibility criteria, treatment is rarely observed exactly at the time of eligibility. Ad-hoc solutions to this timing misalignment can induce bias by incorrectly attributing prior event counts and person-time to treatment. Even if eligibility and treatment are aligned, a terminal event process (e.g. death) often stops the recurrent event process of interest. In practice, both processes can be censored so that events are not observed over the entire followup window. Our approach addresses misalignment by casting it as a time-varying treatment problem: some patients are on treatment at eligibility while others are off treatment but may switch to treatment at a specified time - if they survive long enough. We define and identify an average causal effect estimand under right-censoring. Estimation is done using a g-computation procedure with a joint semiparametric Bayesian model for the death and recurrent event processes. We apply the method to contrast hospitalization rates among patients with different opioid treatments using Medicare insurance claims data.