Bayesian Semiparametric Model for Sequential Treatment Decisions with Informative Timing
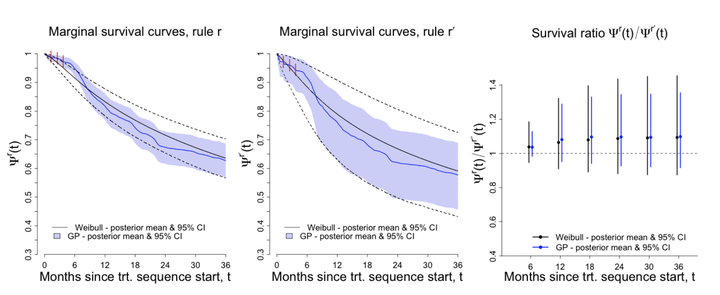 Posterior survival curves under two different dynamic treatment rules and their ratio contrasts
Posterior survival curves under two different dynamic treatment rules and their ratio contrasts
Abstract
We develop a Bayesian semi-parametric model for the estimating the impact of dynamic treatment rules on survival among patients diagnosed with pediatric acute myeloid leukemia (AML). The data consist of a subset of patients enrolled in the phase III AAML1031 clinical trial in which patients move through a sequence of four treatment courses. At each course, they undergo treatment that may or may not include anthracyclines (ACT). While ACT is known to be effective at treating AML, it is also cardiotoxic and can lead to early death for some patients. Our task is to estimate the potential survival probability under hypothetical dynamic ACT treatment strategies, but there are several impediments. First, since ACT was not randomized in the trial, its effect on survival is confounded over time. Second, subjects initiate the next course depending on when they recover from the previous course, making timing potentially informative of subsequent treatment and survival. Third, patients may die or drop out before ever completing the full treatment sequence. We develop a generative Bayesian semi-parametric model based on Gamma Process priors to address these complexities. At each treatment course, the model captures subjects' transition to subsequent treatment or death in continuous time under a given rule. A g-computation procedure is used to compute a posterior over potential survival probability that is adjusted for time-varying confounding. Using this approach, we conduct posterior inference for the efficacy of hypothetical treatment rules that dynamically modify ACT based on evolving cardiac function.