Bayesian Causal Inference
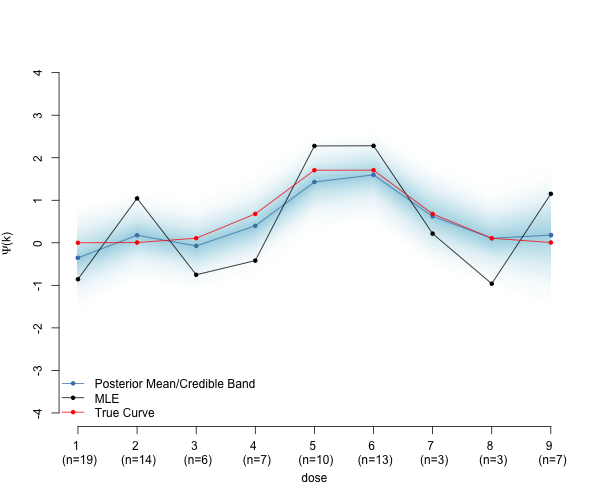 A causal dose-effect curve with an AR(1) prior that smooths the MLE.
A causal dose-effect curve with an AR(1) prior that smooths the MLE.
Causal inference is broadly concerned with estimating parameters governing the causal mechanisms between an intervention or treatment of interest and an outcome. Causal inference provides a framework for 1) constructing different estimands that have explicitly causal, rather than associational, interpretations 2) formulating the assumptions under which we can estimate these using observed data, 3) devising sensitivity analyses around violations of these assumptions, and 4) making valid inferences about these estimans. These are just some of the many advances made in the causal literature.
In practice, causal inference requires complex, high-dimensional models. Here, the Bayesian paradigm has a lot to offer. For instance,
- Shrinking heterogeneous (stratum-specific) causal effects towards an overall average causal effect for sparse strata.
- Sparsity priors such as Horseshoes and Spike-and-Slab that can regularize high-dimensional nuissance parameters. Such parameters are common in g-computation.
- Sensitivity Analyses around causal identification assumptions. Uncertainty about the direction and magnitude of the bias can be expressed via a prior and baked into posterior inference.
See below for work related to Bayesian causal modeling.