Non-parametric Bayes
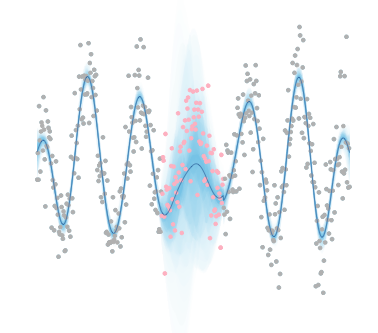 Posterior regression line/band from Gaussian process regression.
Posterior regression line/band from Gaussian process regression.
Bayesian nonparametrics is a powerful class of methods including Gaussian processes, Bayesian Additive Regression Trees (BART), Gamma Processes, Dirichlet Process, etc. The central idea is to abstract away from parameters. For instance, standard methods may assume a regression function is linear, indexed by finitely many slope/intercept parameters. A prior on these finitely many parameters then induces a prior on the regression function. To avoid specifying such restrictive functional form, we need to cut out the middle-man (the parameters) and specify priors over the function directly. Bayesian nonparametrics is characterized by priors over such abstract objects: priors over regressions, priors over baseline hazard functions, prior distributions over distributions themselves.
These methods give you the flexibility of machine learning, with the added benefit uncertainty quantitification via full posterior inference.
See below for work related to nonparametric Bayesian inference.







